| 行业类别 | 格式 | 大小 |
|---|---|---|
| 冀教版八年级数学上册 | pptx | 6 MB |
描述
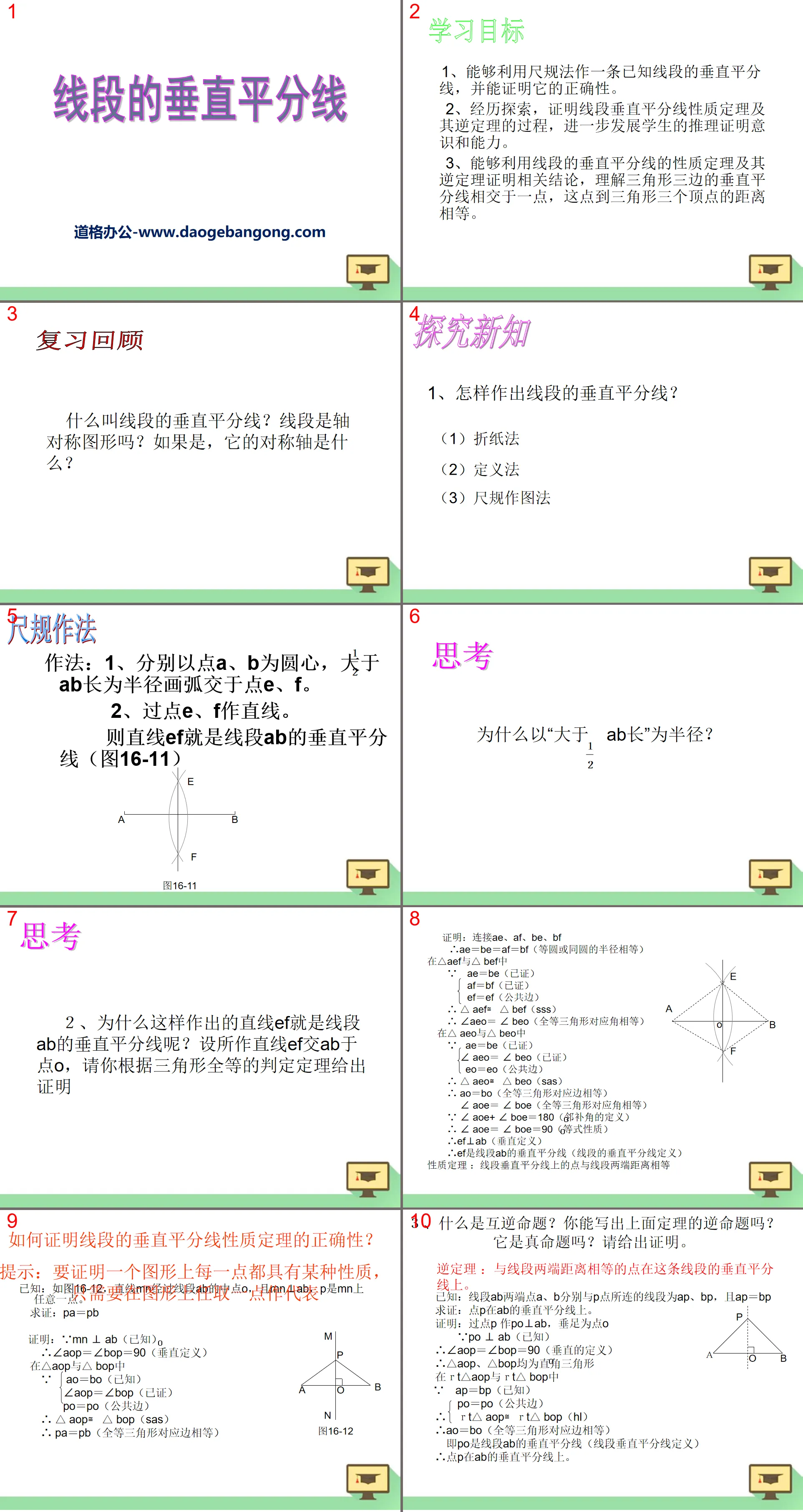
《线段的垂直平分线》PPT课件9
学习目标
1、能够利用尺规法作一条已知线段的垂直平分线,并能证明它的正确性。
2、经历探索,证明线段垂直平分线性质定理及其逆定理的过程,进一步发展学生的推理证明意识和能力。
3、能够利用线段的垂直平分线的性质定理及其逆定理证明相关结论,理解三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等。
复习回顾
什么叫线段的垂直平分线?线段是轴对称图形吗?如果是,它的对称轴是什么?
... ... ...
探究新知
1、怎样作出线段的垂直平分线?
(1)折纸法
(2)定义法
(3)尺规作图法
尺规作法
作法:
1、分别以点A、B为圆心,大于 AB长为半径画弧交于点E、F。
2、过点E、F作直线。
则直线EF就是线段AB的垂直平分线(图16-11)
2、为什么这样作出的直线EF就是线段AB的垂直平分线呢?设所作直线EF交AB于点O,请你根据三角形全等的判定定理给出证明
证明:连接AE、AF、BE、BF∴AE=BE=AF=BF(等圆或同圆的半径相等)
在△AEF与△ BEF中
∵AE=BE(已证)
AF=BF(已证)
EF=EF(公共边)
∴ △ AEF≌ △ BEF(SSS)
∴ ∠AEO= ∠ BEO(全等三角形对应角相等)
在△ AEO与△ BEO中
∵ AE=BE(已证)
∠ AEO= ∠ BEO(已证)
EO=EO(公共边)
∴ △ AEO≌ △ BEO(SAS)
∴ AO=BO(全等三角形对应边相等)
∠ AOE= ∠ BOE(全等三角形对应角相等)
∵ ∠ AOE+ ∠ BOE=180(邻补角的定义)
∴ ∠ AOE= ∠ BOE=90(等式性质)
∴EF⊥AB(垂直定义)
∴EF是线段AB的垂直平分线(线段的垂直平分线定义)
性质定理 :线段垂直平分线上的点与线段两端距离相等
... ... ...
课堂小结
本节课重点学习了两个知识点:
1、线段垂直平分线上的点与线段两端相离相等。
2、与线段两端距离相等的点在这条线段的垂直平分线上。
关键词:线段的垂直平分线教学课件,冀教版八年级上册数学PPT课件下载,八年级数学幻灯片课件下载,线段的垂直平分线PPT课件下载,.PPT格式;
更多关于《 线段的垂直平分线 》PPT课件, 请点击 线段的垂直平分线ppt标签。
《线段的垂直平分线》PPT课件10:
《线段的垂直平分线》PPT课件10 问题 线段的垂直平分线的定义? 线段是轴对称图形么? 怎样做出一条线段的垂直平分线? 定义法; 折纸; 尺规作图法 尺规作图 作法: 1. 分别以点A、B为..
《线段的垂直平分线》PPT课件8:
《线段的垂直平分线》PPT课件8 教学目标 1、能说出线段的垂直平分线的定理和逆定理,会区别运用这两个定理。 2、体会学习数学的方法,观察,概括,验证,比较等在本课时中的应用。 3..
《线段的垂直平分线》PPT课件7:
《线段的垂直平分线》PPT课件7 问题: 1.线段是轴对称图形吗?如果是对称轴是什么? 2.什么是线段的垂直平分线? 3.怎样做出一条线段的垂直平分线? 思考:还有什么方法可以确定线段的..
文件信息
更新时间: 2024-11-16
所属频道:冀教版八年级数学上册
素材版本:PowerPoint2003及以上版本(.ppt)
文件大小:153 KB
显示比例:普屏4:3
附件类型:.rar
本模板属于 数学课件 冀教版八年级数学上册 行业PPT模板
《线段的垂直平分线》PPT课件9 简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板是由文稿PPT提供的商务岗位竞聘通用PPT模板,简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板,下载源文件即可自行编辑修改源文件里的文字和图片,如果想要更多精美商务PPT模板,可以来道格办公。道格办公PPT,海量PPT模板幻灯片素材下载,我们只做精品的PPT模板!
Tips:如果打开模版觉得不合适您全部需求的话,可以检索相关内容「《线段的垂直平分线》PPT课件9 」即可。
Windows系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
Mac系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
相关阅读
更详细的PPT相关的教程、字体的教程可以查看: 点击查看
注意事项
不要在微信、知乎、QQ、内置浏览器下载、请用手机浏览器下载! 如果您是手机用户,请移步电脑端下载!
1、文稿PPT,仅供学习参考,请在下载后24小时删除。
2、如果资源涉及你的合法权益,第一时间删除。
3、联系方式:service@daogebangong.com
《线段的垂直平分线》PPT课件9 由于使用限制,仅供个人学习与参考使用,如需商业使用请到相关官网授权。
(个人非商业用途是指以个人为单位、非商业产品运作的方式,运用该字体完成个人作品的展示,包括但不限于个人论文、简历等作品的设计)
预览效果