九年級數學機率專題解,四大考點分類解析+例題解析+專題練習。機率問題是中考必然會出現的考場之一。對於機率問題,大家在學習過程中並不感到陌生,學習過程中,其關鍵是要同學們對機率的定義以及頻率的區別與聯繫這一重點。學會用機率知識解釋現實生活中的實際問題,這個困難的掌握和突破以及如何把具體的問題轉化為抽象的概念。

其中學習的重點為事件的分類,機率的定義以及和頻率的區別與聯繫。其困難在於對於隨機事件發生的統計規律性的理解。
一、學習目標
1.掌握求機率的兩種方法列舉法與頻率估計法;< /span>
2.掌握求機率的不同方法的應用.
二、知識點總結與梳理
1.隨機事件
(1)確定事件
事先能肯定它一定會發生的事件稱為必然事件,事先能肯定它一定不會發生的事件稱為不可能事件,必然事件和不可能事件都是確定的.

(2)隨機事件
在某些條件下,可能發生也可能不發生的事件,稱為隨機事件.
(3)事件分為確定事件與不確定事件(隨機事件),確定事件又分為必然事件與不可能事件,其中,
①必然事件發生的機率為1,即P(必然事件)=1;
②不可能事件發生的機率為0,即P(不可能事件)=0;
③如果A為不確定事件(隨機事件),則0<P(A) <1.
2.可能性大小

(1)理論計算又分為以下兩種情況:
第一種:只涉及一步實驗的隨機事件發生的機率,如:根據機率的大小與面積的關係,對一類機率模型進行的計算;第二種:透過列表法、列舉法、樹狀圖來計算涉及兩步或兩步以上實驗的隨機事件發生的機率,如:配紫色,對遊戲是否公平的計算.
(2)實驗估算又分為以下兩種情況:
第一種:利用實驗的方法進行機率估算.要知道當實驗次數非常大時,實驗頻率可作為事件發生的機率的估計值,即大量實驗頻率穩定於理論機率.
第二種:利用模擬實驗的方法進行機率估算.如,利用計算機產生隨機數來模擬實驗.
3.機率的意義
(1)一般地,在大量重複實驗中,如果事件A發生的頻率mn會穩定在某個常數p附近,那麼這個常數p就叫做事件A的機率,記為P(A)=p.

(2)機率是頻率(多)的波動穩定值,是事件發生可能性大小的量的表現.
(3)機率取值範圍:_________.
(4)必然發生的事件的機率P(A)=1;不可能發生事件的機率P(A)=0.
(4)事件發生的可能性越大,機率越接近1,事件發生的可能性越小,機率越接近0.
(5)透過設計簡單的機率模型,在不確定的情境中做出合理的決策;機率與實際生活聯繫密切,透過理解什麼是遊戲對雙方公平,用機率的語言說明遊戲的公平性,並能依要求設計遊戲的機率模型,以及結合具體實際問題,體會機率與統計之間的關係,可以解決一些實際問題.
4.求機率的方法
(1)用_______求機率
(2)利用________機率
5.遊戲公平性
(1)判斷遊戲公平性需要先計算每個事件的機率,然後比較機率的大小,機率相等就公平,否則就不公平.
(2)機率=所求情況數總情況數.

三、四大考點+經典例題解析
1.事件與機率
【例1】下列事件是必然發生事件的是( )
A.打開電視機,正在轉播足球比賽
B.小麥的畝產量一定為1000公斤
C.在只裝有5個紅球的袋中摸出1球,是紅球
D.農曆十五的晚上一定能看到圓月
【解析】必然事件的定義是一定會發生的事,可選出答案。

2. 利用面積求機率
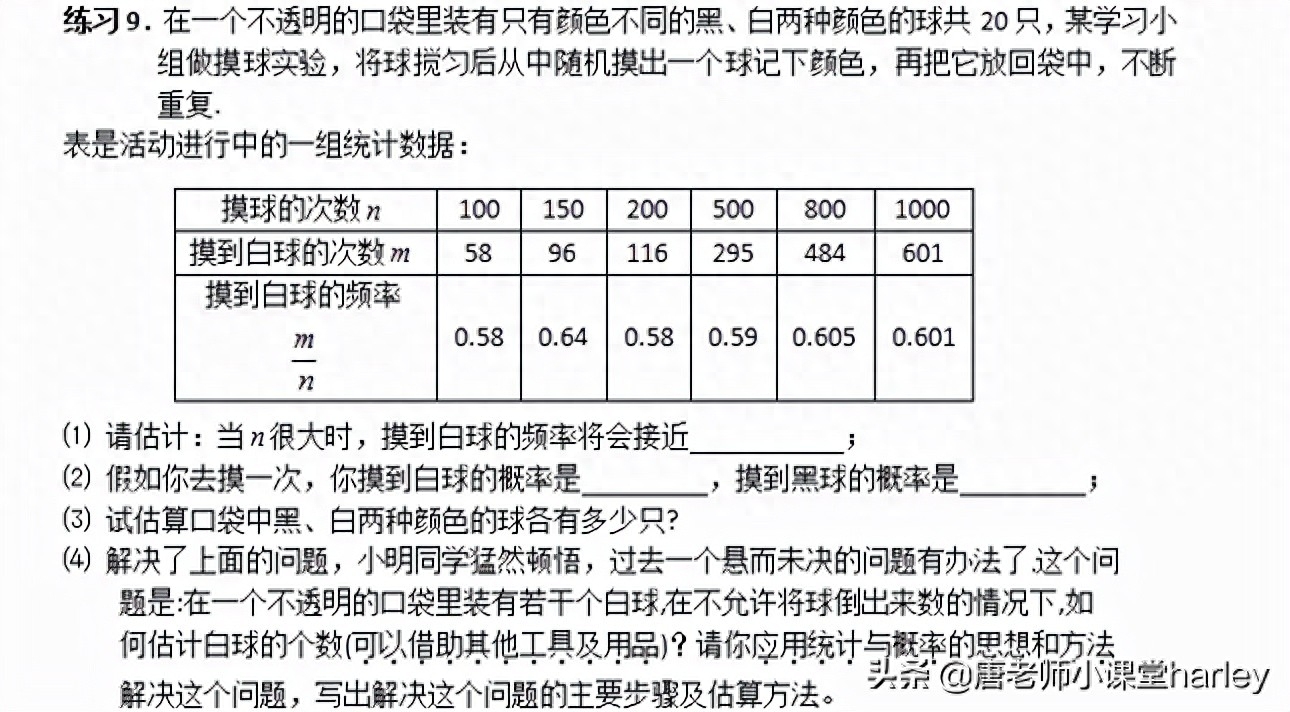
【例3】如圖是一個被等分成6個扇形可自由轉動的轉盤,轉動轉盤,當轉盤停止後,指針指向紅色區域的機率是多少?

【解析】圓形分成6部分,其中3部分是紅色,就可以求出機率。


3.列舉法求機率
【例4】有兩個可以自由轉動的均勻轉盤AB,都被分成了3等份,並在每份內均標有數字,
如圖所示.規則如下:
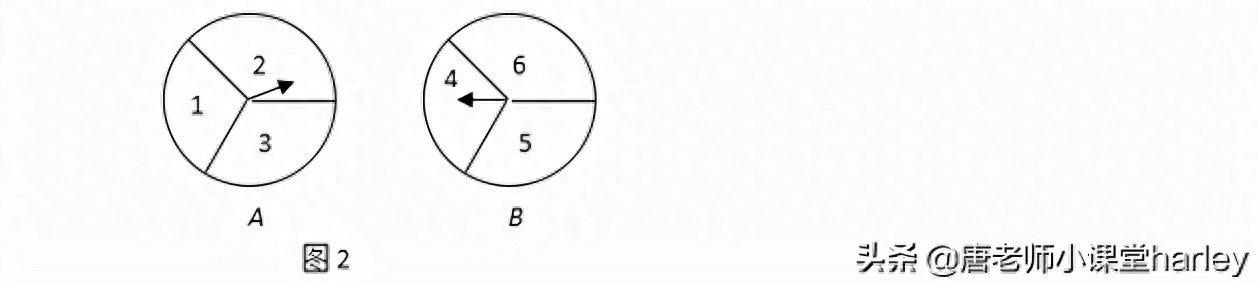
①分別轉動轉盤A\B;
②兩個轉盤停止後,將兩個指針所指的數字相乘(若指針停止在等分線上,那麼重裝一次,直到指針指向某一份為止)。
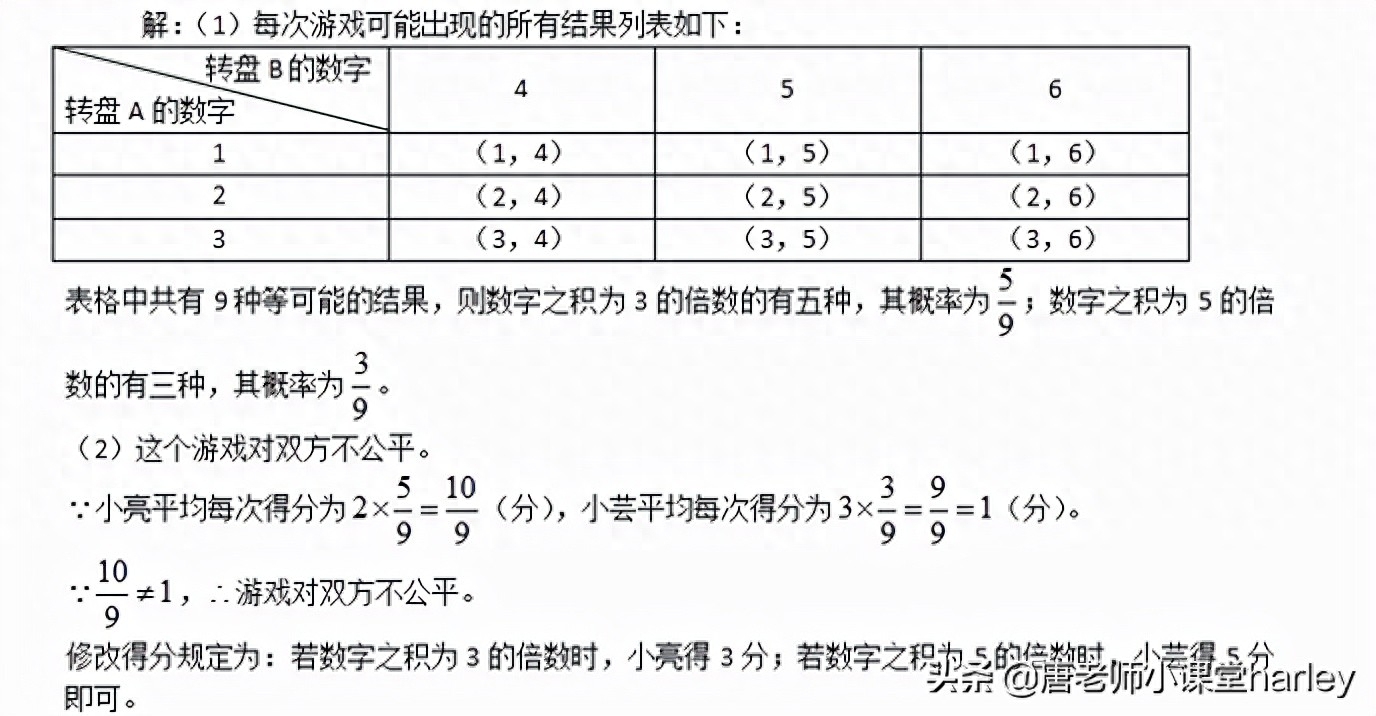
(1)用列表法(或樹狀圖)分別求出數字之積為3的倍數和數字積為5的倍數的機率;
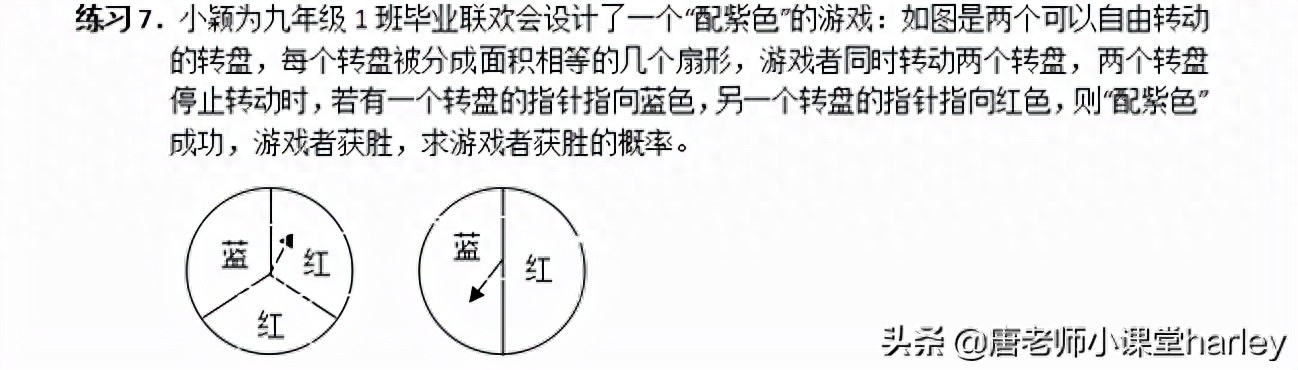
(2)小亮和小芸想用這兩個轉盤做遊戲,他們規定:數字之積為3的倍數時,小亮得2分;數字之積為5的倍數時,小芸得3分.這個遊戲對雙方公平嗎?請說明理由;認為不公平的,試修改得分規定,使遊戲對雙方公平。

【解析】(1)求兩個轉盤的數字積的問題,可以把所有情況羅列出來,再找對應的結論所佔的機率即可。 (2)分別確定每種情況的機率,再確定是否公平。
4. 頻率法估算機率
【例5】小明為了檢驗兩枚六個面分別刻有點數1 、2、3、4、5、6的正六面體骰子的質量是否都合格,在相同的條件下,同時拋兩枚骰子20000次,結果發現兩個朝上面的點數和是7的次數為20次.你認為這兩枚骰子質量是否都合格(合格標準為:在相同條件下拋骰子時,骰子各個面朝上的機會相等)?並說明理由。

【解析】本題可透過分別計算出現兩個朝上點數和為7的機率和實驗20000次出現兩個
朝上點數和為7的頻率,然後依據大量重複實驗時事件發生頻率與事件發生機率的差距將很小,來確定品質是否都合格。
透過以上對機率四大考點以及例題解析的講解,同學們對於機率題型的了解基本上已比較全面。在學習的過程當中,同學們更要專注於對其概念及規律性的理解,這是大家比較困難或是學起來難以理解的部分。針對每一個考點,同學們都要進行細緻的分析及了解其考點的。規律性才能掌握其做題的方法,從而不失去這部分的分數。
文章為用戶上傳,僅供非商業瀏覽。發布者:Lomu,轉轉請註明出處: https://www.daogebangong.com/zh-Hant/articles/detail/jiu-nian-ji-shu-xue-gai-lyu-zhuan-ti-jiang-jie-si-da-kao-dian-fen-lei-jie-xi-li-ti-jie-xi-zhuan-ti-lian-xi.html

 支付宝扫一扫
支付宝扫一扫 
评论列表(196条)
测试