"Pouvoirs des nombres rationnels" Didacticiel PPT sur les nombres rationnels 3简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板是由文稿PPT提供的商务岗位竞聘通用PPT模板,简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板,下载源文件即可自行编辑修改源文件里的文字和图片,如果想要更多精美商务PPT模板,可以来道格办公。道格办公PPT,海量PPT模板幻灯片素材下载,我们只做精品的PPT模板!
| 文件名 如何下载使用 | 下载次数 | Points de téléchargement | 下载地址 |
|---|---|---|---|
| "Pouvoirs des nombres ra... | 15650次 | 0.00 | Téléchargement gratuit |
Tips:如果打开模版觉得不合适您全部需求的话,可以检索相关内容「"Pouvoirs des nombres rationnels" Didacticiel PPT sur les nombres rationnels 3」即可。
Windows系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
Mac系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
相关阅读
更详细的PPT相关的教程、字体的教程可以查看: 点击查看
注意事项
不要在微信、知乎、QQ、内置浏览器下载、请用手机浏览器下载! 如果您是手机用户,请移步电脑端下载!
1、文稿PPT,仅供学习参考,请在下载后24小时删除。
2、如果资源涉及你的合法权益,第一时间删除。
3、联系方式:service@daogebangong.com
"Pouvoirs des nombres rationnels" Didacticiel PPT sur les nombres rationnels 3由于使用限制,仅供个人学习与参考使用,如需商业使用请到相关官网授权。
(个人非商业用途是指以个人为单位、非商业产品运作的方式,运用该字体完成个人作品的展示,包括但不限于个人论文、简历等作品的设计)
Lecture associée
更详细的PPT相关的教程、字体的教程可以查看:Veuillez cliquer pour voir










Faire autorité PPT简介
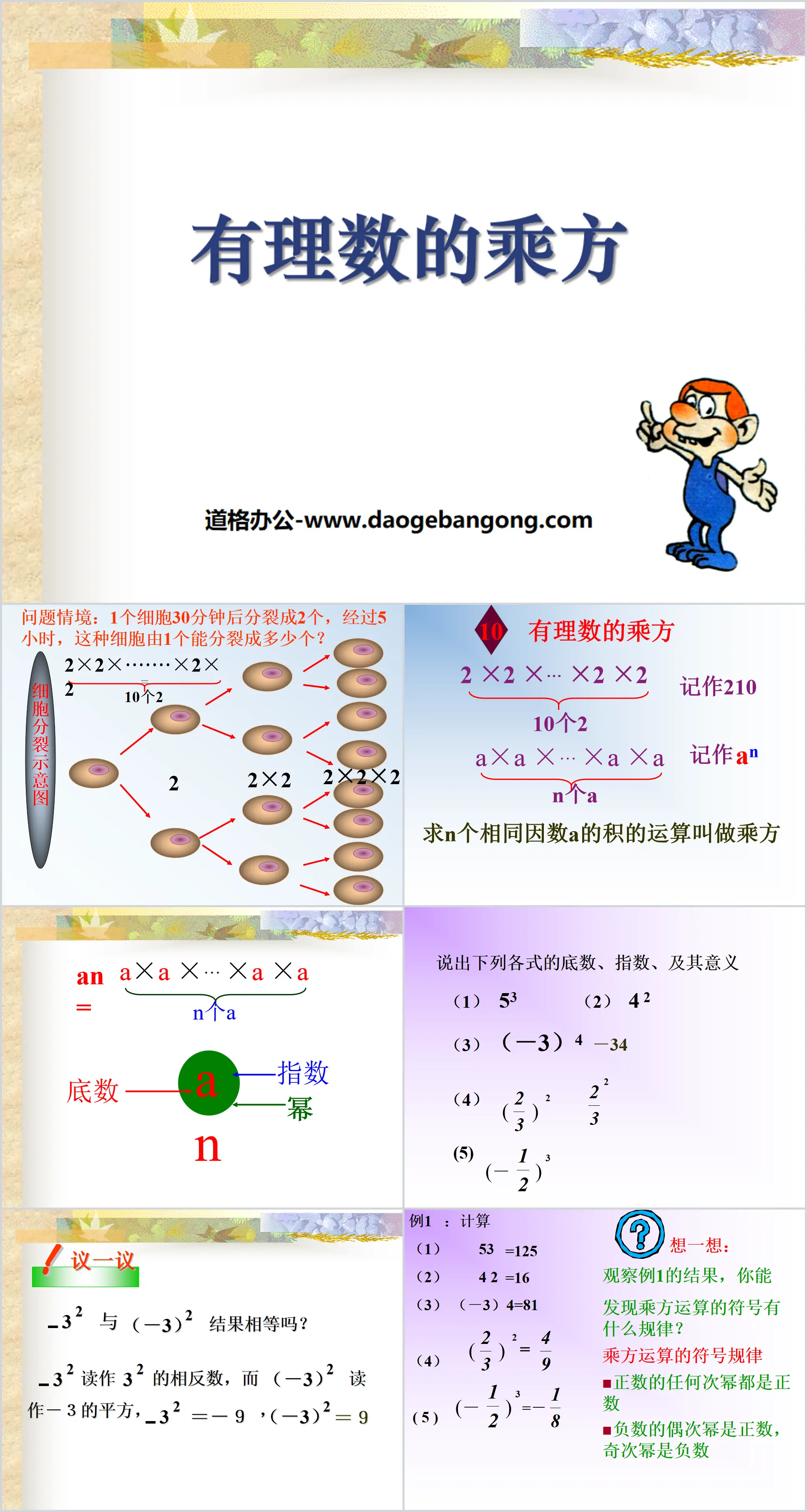
"Pouvoirs des nombres rationnels" Didacticiel PPT sur les nombres rationnels 3
Pensez-y :
En observant les résultats de l'exemple 1, pouvez-vous trouver des règles dans les signes des opérations d'exponentiation ?
Règles de signature pour les opérations d'exponentiation
Toute puissance d'un nombre positif est un nombre positif
Les nombres négatifs élevés à des puissances paires sont des nombres positifs, et les puissances impaires élevées à des nombres négatifs sont des nombres négatifs.
Avis:
(1) Lorsque vous écrivez la puissance d’un nombre négatif, vous devez mettre le nombre négatif entier (avec le symbole) entre parenthèses. C’est également la façon d’identifier la base.
(2) Lors de l’écriture d’une puissance d’une fraction, la fraction entière doit être mise entre parenthèses.
1. Décidez si les questions suivantes sont correctes ou non
①2³=2 ×3 ( )
②2+2+2=2³ ( )
③2³=2×2 ×2 ( )
2. Coupez la moitié d'un bâton d'un mètre de long la première fois, puis coupez la moitié restante la deuxième fois. Si cela continue, quelle sera la longueur du bâton restant après la cinquième fois ?
Le mont Everest est le plus haut sommet du monde, avec une altitude de 8 848 mètres.
Un morceau de papier assez grand d'une épaisseur de 0,1 mm, plié en deux 30 fois de suite, peut être plus épais que le mont Everest. Est-ce vrai ?
Mots-clés : didacticiel sur les nombres rationnels, didacticiel sur l'exponentiation des nombres rationnels, didacticiel PPT de mathématiques de septième année de New People's Education Edition, téléchargement de didacticiel de diapositives de mathématiques de septième année, téléchargement de didacticiel PPT sur les nombres rationnels, téléchargement de didacticiel PPT sur les exposants de nombres rationnels, format .ppt
Pour plus d'informations sur le didacticiel PPT « Les nombres rationnels alimentés par des nombres rationnels », veuillez cliquer sur la balise ppt Les nombres rationnels alimentés par des nombres rationnels.
Didacticiel PPT « Le pouvoir des nombres rationnels » 4 :
« Les pouvoirs des nombres rationnels » Didacticiel PPT 4 Exploration collaborative 1 : Le pliage en deux deux fois peut être coupé en 4 morceaux, soit 22 morceaux ; Le pliage en deux trois fois peut être coupé en 8 morceaux, soit 222 morceaux ; Combien de morceaux peut-on couper s’il est plié en deux 10 fois ? Veuillez utiliser une formule pour l'exprimer (pas besoin de calculer le résultat). Si vous le pliez en deux 100 fois, la formule...
Didacticiel PPT « Le pouvoir des nombres rationnels » 3 :
"Puissance des nombres rationnels" Didacticiel PPT 3 Objectifs pédagogiques Connaissances et compétences 1. Expérimenter le processus de génération du concept de puissance à travers des exemples 2. Comprendre les concepts de puissance, de puissance, d'exposant et de base, et maîtriser la représentation de la puissance et pouvoir ; 3. Comprendre la loi symbolique du pouvoir et être capable de mener des actions rationnelles...
Didacticiel PPT « Le pouvoir des nombres rationnels » 2 :
"Les pouvoirs des nombres rationnels" Didacticiel PPT 2 Il y a un morceau de papier d'une épaisseur de 1 micron Après l'avoir plié en deux 50 fois, imaginez quelle est son épaisseur ? ⑴ Après avoir plié deux fois, quelle est l'épaisseur de microns ? 221 ⑵ Après l'avoir plié en deux trois fois, quelle est l'épaisseur de microns ? 2221 ⑶ Après avoir plié en deux 4 fois, l'épaisseur...