"Distance de freinage et fonction quadratique" Fonction quadratique Didacticiel PPT 2

描述

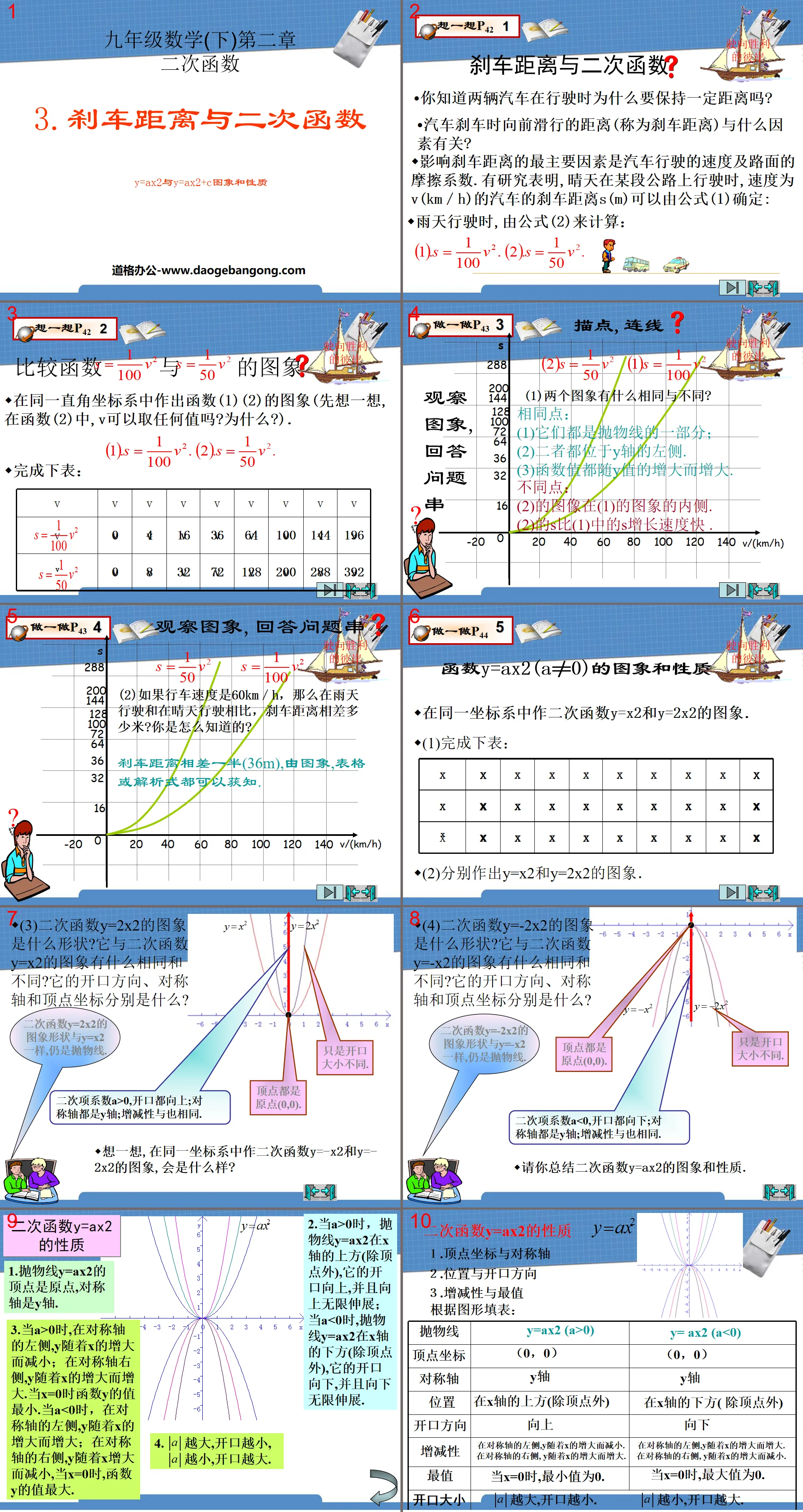
"Distance de freinage et fonction quadratique" Fonction quadratique Didacticiel PPT 2

réfléchis-y

Savez-vous pourquoi deux voitures doivent garder une certaine distance lorsqu’elles conduisent ?

Quels facteurs déterminent la distance parcourue par une voiture lors du freinage (appelée distance de freinage) ?

Les facteurs les plus importants affectant la distance de freinage sont la vitesse de la voiture et le coefficient de frottement de la surface de la route. Des études ont montré que lors de la conduite sur un certain tronçon de route par une journée ensoleillée, la distance de freinage s (m) d'une voiture. avec une vitesse de v (km/h) peut être calculé par la formule (1) détermine :

Lors de la conduite les jours de pluie, il est calculé par la formule (2) :

（1）s=1/100v² （2）s=1/50v²

Fais-le

L'image et les propriétés de la fonction y=ax2(a≠0)

Dessinez les graphiques des fonctions quadratiques y=x2 et y=2x2 dans le même système de coordonnées.

(1) Complétez le tableau suivant :

(2) Créez respectivement les images de y=x2 et y=2x2.

(3) Quelle est la forme du graphique de la fonction quadratique y=2x2 ? Quelles sont les similitudes et les différences entre celui-ci et le graphique de la fonction quadratique y=x2 ? Quelles sont sa direction d'ouverture, son axe de symétrie et ses coordonnées de sommet ?

La forme du graphique de la fonction quadratique y=2x2 est la même que celle de y=x2, qui est toujours une parabole.

Pensez-y, qu'est-ce que cela donnerait de dessiner les images des fonctions quadratiques y=-x2 et y=-2x2 dans le même système de coordonnées ?

Propriétés de la fonction quadratique y=ax2

1. Le sommet de la parabole y=ax2 est l'origine et l'axe de symétrie est l'axe y.

2. Lorsque a>0, la parabole y=ax2 est au-dessus de l'axe des x (sauf pour le sommet), son ouverture est vers le haut, et elle s'étend vers le haut à l'infini. Lorsque a<0, la parabole y=ax2 est en dessous de x ; -axe (sauf pour le sommet) en dehors du sommet), son ouverture est vers le bas, et il s'étend vers le bas à l'infini.

3. Lorsque a>0, sur le côté gauche de l'axe de symétrie, y diminue à mesure que x augmente ; sur le côté droit de l'axe de symétrie, y augmente à mesure que x augmente. Lorsque x=0, la fonction y a la plus petite valeur. Lorsque a<0, sur le côté gauche de l'axe de symétrie, y augmente à mesure que x augmente ; sur le côté droit de l'axe de symétrie, y diminue à mesure que x augmente, lorsque x=0 , la valeur de la fonction y est la plus grande.

4. Plus le « a » est grand, plus l'ouverture est petite.

Plus le « a » est petit, plus l’ouverture est grande.

Je pense, je progresse

Tracez le graphique de la fonction quadratique y=2x²+1 et le graphique de la fonction quadratique y=2x² dans le même système de coordonnées.

Quelle est la relation entre le graphique de la fonction quadratique y=2x²+1 et le graphique de la fonction quadratique y=2x² ? S'agit-il de graphiques à symétrie axiale ? Quelles sont sa direction d'ouverture, son axe de symétrie et ses coordonnées de sommet ? le graphique regarde.

Résumé et extension

La relation entre la fonction quadratique y=ax²+c et =ax²

1. Points similaires : (1) Les images sont toutes des paraboles, avec la même forme et la même direction d'ouverture.

(2) Ce sont toutes des figures à symétrie d'axe et les axes de symétrie sont tous l'axe des y.

(3) Il existe une valeur maximale (grande ou petite).

(4) Lorsque a>0, l'ouverture est vers le haut. Sur le côté gauche de l'axe y, y diminue avec l'augmentation de x. Sur le côté droit de l'axe y, y augmente avec l'augmentation de x. a<0, Avec l'ouverture vers le bas, sur le côté gauche de l'axe y, y augmente à mesure que x augmente, et sur le côté droit de l'axe y, y diminue à mesure que x augmente.

2. Différents points : (1) Les sommets sont différents : (0,c), (0,0).

(2) Les valeurs maximales sont différentes : respectivement c et 0.

3. Connexion : L'image de y=ax²+c(a≠0) peut être considérée comme l'image de y=ax² obtenue en décalant l'unité entière le long de l'axe y de c unités (quand c>0 Translate. vers le haut ; lorsque c<0, traduire vers le bas).

exercice

1． Quelle est la relation entre les graphiques de la fonction quadratique y=-3x² et y=3x² ? Est-ce une figure à symétrie axiale ? Quelles sont sa direction d'ouverture, son axe de symétrie et ses coordonnées de sommet ? nécessaire. Jetez un oeil.

Qu'en est-il des fonctions quadratiques y=-1/2x² et y=1/2x² ?

2. Quelle est la relation entre le graphique de la fonction quadratique y=3x²+1/2 et y=3x² ? Est-ce une figure à symétrie axiale ? Quelles sont sa direction d'ouverture, son axe de symétrie et ses coordonnées de sommet ? , Jetez un œil au croquis.

Qu'en est-il des fonctions quadratiques y=-1/2x²+3 et y=-1/2x² ?

Mots-clés : didacticiel d'enseignement de la fonction quadratique, distance de freinage et didacticiel d'enseignement de la fonction quadratique, didacticiel PPT de neuvième année, édition de l'Université normale de Pékin, téléchargement du didacticiel de diapositives de mathématiques de neuvième année, téléchargement du didacticiel PPT de la fonction quadratique, téléchargement du didacticiel PPT de la distance de freinage et de la fonction quadratique, . format ppt

Pour plus d'informations sur le didacticiel PPT « Distance de freinage de la fonction quadratique et fonction quadratique », veuillez cliquer sur la balise ppt de la fonction quadratique ppt Distance de freinage et de la fonction quadratique.

"Distance de freinage et fonction quadratique" Didacticiel PPT sur la fonction quadratique 3 :

"Distance de freinage et fonction quadratique" Didacticiel PPT sur la fonction quadratique 3 Pensez-y. Savez-vous pourquoi deux voitures gardent une certaine distance lorsqu'elles conduisent. Quels facteurs sont liés à la distance qu'une voiture avance lors du freinage (appelée distance de freinage) ? facteur le plus important affectant la distance de freinage.

Didacticiel PPT sur la fonction quadratique « Distance de freinage et fonction quadratique » :

"Distance de freinage et fonction quadratique" Fonction quadratique Objectifs d'apprentissage du didacticiel PPT 1. Connaissances et compétences 1. Les images de y=ax2 et y=ax2+c peuvent être réalisées. et étudier leurs propriétés. 2. Comparez les similitudes et les différences entre les images de y=ax2 et y=ax2+c et y=x2. Comprendre la paire a et c.

文件信息

更新时间: 2024-11-21

本模板属于 数学课件 北师大九年级数学下册 行业PPT模板

预览效果