Cours PPT « Application des équations linéaires à deux variables »

描述

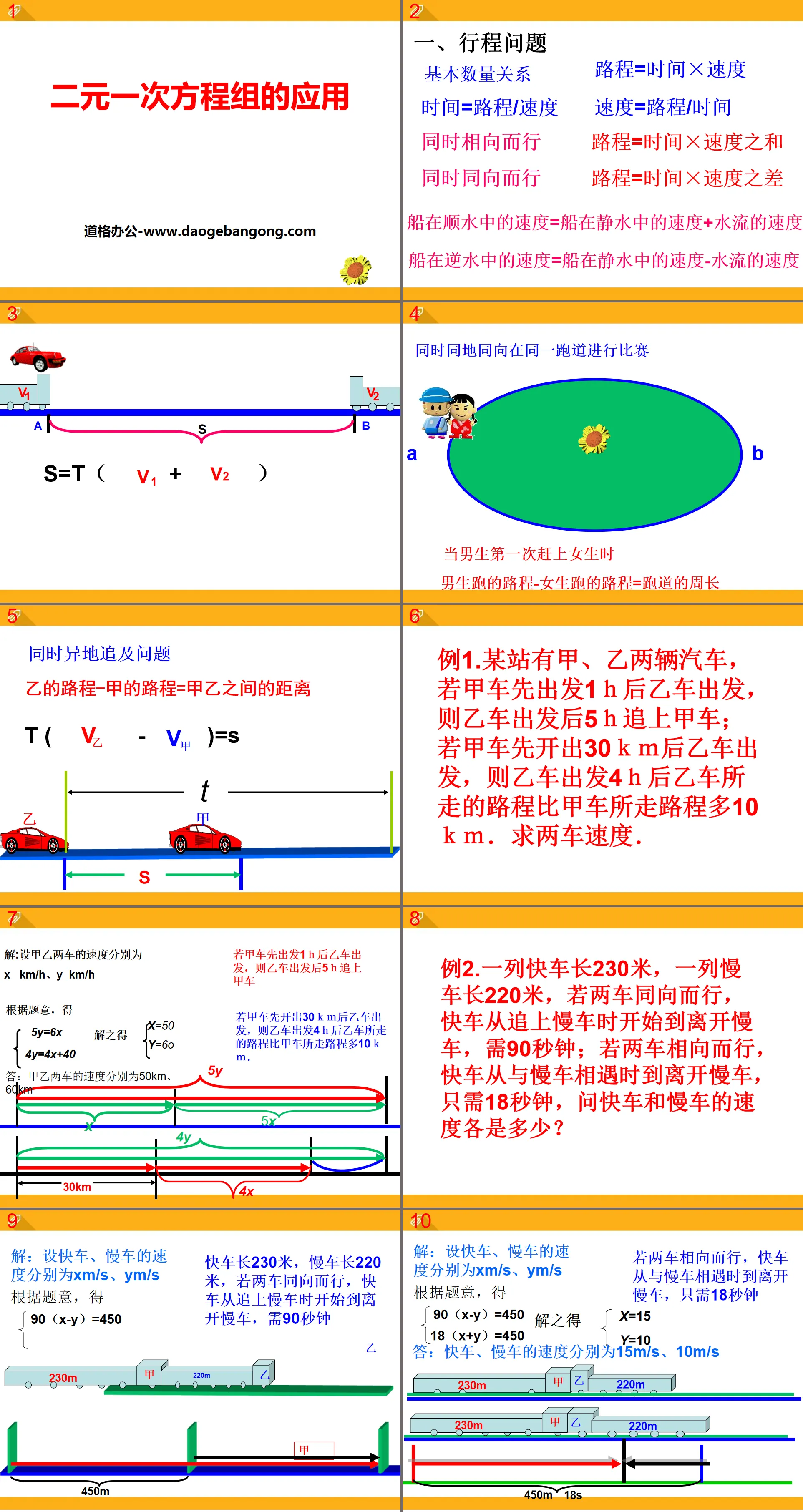
Cours PPT « Application des équations linéaires à deux variables »

Première partie : Problèmes d'itinéraire

relation quantitative de base

distance = temps x vitesse

temps=distance/vitesse

vitesse=distance/temps

En voyageant dans la même direction au même moment, distance = somme du temps x vitesse

En voyageant dans la même direction au même moment, distance = temps × différence de vitesse

La vitesse du bateau en eau calme = la vitesse du bateau en eau calme + la vitesse du courant

La vitesse du bateau en eau amont = la vitesse du bateau en eau calme - la vitesse du courant

PPT sur l'application des équations linéaires à deux variables, partie 2 : analyse d'exemples

Exemple 1. Il y a deux voitures A et B à une certaine station. Si la voiture A démarre en premier, puis la voiture B démarre une heure plus tard, la voiture B rattrapera la voiture A 5 heures après le départ. Si la voiture A parcourt d'abord 30 km, puis la voiture B démarre, alors la voiture B rattrapera la voiture A. 4 heures après le départ, la distance parcourue par le véhicule B est 10 km plus longue que la distance parcourue par le véhicule A. Trouvez la vitesse des deux voitures.

Exemple 2. Un train express mesure 230 mètres de long et un train lent 220 mètres de long. Si les deux trains circulent dans la même direction, il faudra 90 secondes entre le moment où le train express rattrape le train lent et celui où il quitte le train lent. Il ne faut que 18 secondes pour quitter le train local lorsqu'ils se rencontrent. Quelles sont les vitesses du train express et du train local ?

Exemple 3. Deux personnes A et B s'entraînent à courir sur une piste circulaire d'une circonférence de 400 m. Si elles partent dans des directions opposées, elles se rencontreront toutes les 2,5 minutes ; si elles partent dans la même direction, elles se rencontreront toutes les 10 minutes. On suppose que la vitesse des deux personnes ne change pas et que A est plus rapide que B. Lentement, trouvez la vitesse de A et B.

Exemple 4. On sait que la distance entre les deux jetées A et B est de 240 km. Un navire de proue navigue entre les deux jetées A et B. Il lui faut 4 heures pour naviguer avec le courant et 6 heures pour naviguer à contre-courant. Trouvez la distance du navire en eau calme, la vitesse et la vélocité de l'écoulement de l'eau.

PPT sur l'application des équations linéaires à deux variables, troisième partie : problèmes d'ingénierie

Charge de travail = temps de travail × efficacité du travail

Heures de travail = charge de travail/efficacité du travail

Efficacité du travail = charge de travail/temps de travail,

Exemple 1. Un ouvrier avait initialement prévu de traiter un lot de pièces dans un délai limité. Si 10 pièces sont traitées par heure, le travail peut être terminé en 3 pièces ; si 11 pièces sont traitées par heure, le travail peut être terminé 1 heure avant la date prévue. Combien de pièces contient ce lot ? Combien d'heures faudra-t-il pour terminer le travail selon le plan initial ?

Solution : Supposons qu'il y ait x pièces dans ce lot et qu'il faille y heures pour les terminer selon le plan initial. Selon le sens de la question, nous obtenons

10y=x+3

11(y-1)=x

solution

X=77

Y=8

Réponse : Il y a 77 pièces dans ce lot, et il faudra 8 heures pour les terminer comme prévu.

PPT sur l'application des équations linéaires à deux variables, partie 4 : enjeux économiques des matières premières

Somme du principal et des intérêts = principal + intérêts

Intérêt = capital × taux d'intérêt annuel × nombre de périodes × impôt sur les intérêts

Impôt sur les revenus d'intérêts = montant des intérêts × 20�

Exemple 1 Li Ming a épargné 2 000 yuans et 1 000 yuans sous deux formes différentes. Au bout d'un an, il les a retirés tous les trois. Après déduction des intérêts et de l'impôt sur le revenu, il a pu obtenir un intérêt de 43,92 yuans. On sait que la somme des taux d'intérêt annuels de ces deux types d'épargne est de 3,24. Question : Quel est le taux d'intérêt annuel pour chaque type d'épargne ? (Remarque : impôt sur le revenu des intérêts payable par les citoyens = montant des intérêts × 20�)

Solution : Supposons que les taux d'intérêt annuels de ces deux épargnes soient respectivement x et y. D'après la question, on obtient

x+y=3. 24%

2000x80%+1000y80%=43.92

solution

x=2,25%

y=0,99%

Réponse : Les taux d’intérêt annuels pour ces deux types d’épargne sont respectivement de 2,25 % et de 0,09 %.

Mots clés : Téléchargement gratuit du logiciel de cours de mathématiques PPT Hebei Education Edition pour la septième année, volume 2, téléchargement PPT de l'application des équations linéaires à deux variables, format .PPT ;

Pour plus d'informations sur le cours PPT « Applications des systèmes d'équations linéaires à deux variables », veuillez cliquer sur la balise ppt « Applications des systèmes d'équations linéaires à deux variables ».

« Applications des systèmes d'équations quadratiques » PPT :

"Applications des équations linéaires à deux variables" PPT Première partie : Passez en revue le passé et apprenez le nouveau. Énumérez les étapes de base pour résoudre des problèmes verbaux avec des équations linéaires à une variable. Quelle est la clé pour résoudre des problèmes verbaux à l'aide d'équations ? Trouvez la relation d'équivalence. Le problème de deux chevaux portant une charge est une question largement répandue dans l'Inde ancienne.

文件信息

更新时间: 2024-10-29

本模板属于 数学课件 冀教版七年级数学下册 行业PPT模板

预览效果