| 行业类别 | 格式 | 大小 |
|---|---|---|
| 北师大版八年级数学上册 | pptx | 6 MB |
描述
Cours PPT « Définition et proposition » Preuve de lignes parallèles (Leçon 2), 21 pages au total.
Première partie : Objectifs d'apprentissage
Théorèmes et axiomes
prouver
Définition et proposition PPT, partie 2 : Comprendre les nouvelles connaissances
Points de connaissance Théorèmes et axiomes
1. En fait, dans l'histoire du développement des mathématiques, les mathématiciens ont également rencontré des problèmes similaires. Au 3e siècle avant J.-C., les gens avaient accumulé une grande quantité de connaissances mathématiques. Sur cette base, l'ancien mathématicien grec Euclide (Euclide) vers 300 avant J.-C.) a écrit un livre intitulé "Éléments". Afin d'illustrer la justesse de chaque conclusion, il a fait des innovations audacieuses lors de la rédaction de ce livre : il a sélectionné certains termes mathématiques et certaines propositions vraies reconnues servent de point de départ et de base pour vérifier d'autres propositions. Les termes mathématiques qu'ils contiennent sont appelés noms originaux, et les propositions vraies reconnues sont appelées axiomes. En plus des axiomes, la vérité ou la fausseté d'autres propositions doit être jugée par un raisonnement déductif.
Preuve de points de connaissance
Le processus de raisonnement déductif est appelé une preuve, et une proposition prouvée est appelée un théorème. Chaque théorème ne peut être prouvé qu'à l'aide d'axiomes, de définitions et de propositions dont la vérité a été prouvée.
Les différences et les liens entre les définitions, les propositions, les faits de base (axiomes) et les théorèmes :
(1) Connexion : Ces quatre éléments sont tous des propositions.
(2) Différence : les définitions, les faits fondamentaux et les théorèmes sont tous des propositions vraies et peuvent être utilisés comme base pour juger plus avant de la véracité ou de la fausseté d'autres propositions, mais les faits fondamentaux sont la base la plus originale ; et les propositions ne sont pas nécessairement des propositions vraies, elles ne peuvent donc pas être utilisées comme base supplémentaire pour juger de la véracité ou de la fausseté d'autres propositions. La base pour juger si d'autres propositions sont vraies ou fausses.
Définition et proposition PPT, partie 3 : résumé du cours
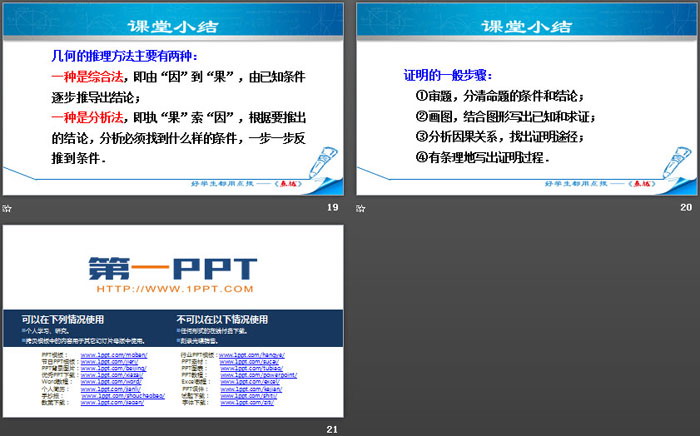
Il existe deux principales méthodes de raisonnement géométrique :
La première est la méthode globale, c'est-à-dire allant de la « cause » à l'« effet », en déduisant progressivement la conclusion à partir des conditions connues ;
La première méthode est la méthode analytique, qui consiste à rechercher la « cause » à partir de l'« effet ». En fonction de la conclusion à tirer, on analyse les conditions à trouver et on remonte les conditions étape par étape.
Étapes générales pour la preuve :
① Revoyez le sujet et distinguez les conditions et les conclusions de la proposition ;
②Dessinez des images et écrivez ce qui est connu et vérifié sur la base des images ;
③Analyser les relations de cause à effet et trouver des moyens de les prouver ;
④Rédigez le processus de preuve de manière organisée.
Mots-clés : Téléchargement gratuit de la version PPT du cours de mathématiques de huitième année de l'Université normale de Pékin, téléchargement PPT des définitions et des propositions, téléchargement PPT de la preuve des droites parallèles, format .PPT ;
Pour plus d'informations sur le cours PPT « Preuve, définition et proposition de lignes parallèles », veuillez cliquer sur l'onglet PPT Définition et proposition de preuve de lignes parallèles.
Téléchargement du PPT « Définition et proposition » Preuve de parallèles :
"Définition et proposition" Preuve de lignes parallèles Téléchargement PPT, 12 pages au total. Première partie : Points de connaissances de base Point de connaissance 1 Définition et proposition 1. Les phrases suivantes appartiennent à la définition (D) A. Deux points déterminent une ligne droite B. Deux lignes parallèles sont interceptées par une ligne droite.
Cours PPT « Définition et proposition » Preuve de parallèles (Leçon 1) :
Cours PPT « Définitions et propositions » Preuve de parallélisme (Leçon 1), 24 pages au total. La première partie du contenu : Objectifs d'apprentissage, définitions, propositions et composition des propositions, classification des propositions... Définition et propositions PPT, la deuxième partie du contenu : Compréhension de nouvelles connaissances, points de connaissance, détermination...
« Définition et proposition » Preuve de parallèles entre lignes PPT (Leçon 2) :
"Définition et proposition" Preuve de parallèles (Leçon 2), 13 pages au total. Première partie : Objectifs d'apprentissage 1. Comprendre les concepts d'axiomes, de théorèmes et de preuves et comprendre les axiomes utilisés dans cet ensemble de manuels. (Points clés) 2. Comprendre la nécessité de la preuve de proposition et expérimenter les mathématiques.
文件信息
更新时间: 2024-11-22
本模板属于 数学课件 北师大版八年级数学上册 行业PPT模板
Cours PPT « Définition et proposition » Preuve de parallèles (Leçon 2)简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板是由文稿PPT提供的商务岗位竞聘通用PPT模板,简约校园招聘活动策划方案总结企事业单位招聘宣传演讲会PPT模板,下载源文件即可自行编辑修改源文件里的文字和图片,如果想要更多精美商务PPT模板,可以来道格办公。道格办公PPT,海量PPT模板幻灯片素材下载,我们只做精品的PPT模板!
Tips:如果打开模版觉得不合适您全部需求的话,可以检索相关内容「Cours PPT « Définition et proposition » Preuve de parallèles (Leçon 2)」即可。
Windows系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
Mac系统模版使用方法
直接解压文件后使用office 或者 wps即可使用
相关阅读
更详细的PPT相关的教程、字体的教程可以查看: 点击查看
注意事项
不要在微信、知乎、QQ、内置浏览器下载、请用手机浏览器下载! 如果您是手机用户,请移步电脑端下载!
1、文稿PPT,仅供学习参考,请在下载后24小时删除。
2、如果资源涉及你的合法权益,第一时间删除。
3、联系方式:service@daogebangong.com
Cours PPT « Définition et proposition » Preuve de parallèles (Leçon 2)由于使用限制,仅供个人学习与参考使用,如需商业使用请到相关官网授权。
(个人非商业用途是指以个人为单位、非商业产品运作的方式,运用该字体完成个人作品的展示,包括但不限于个人论文、简历等作品的设计)
预览效果