"Trois vues d'objets" Didacticiel PPT 2

描述

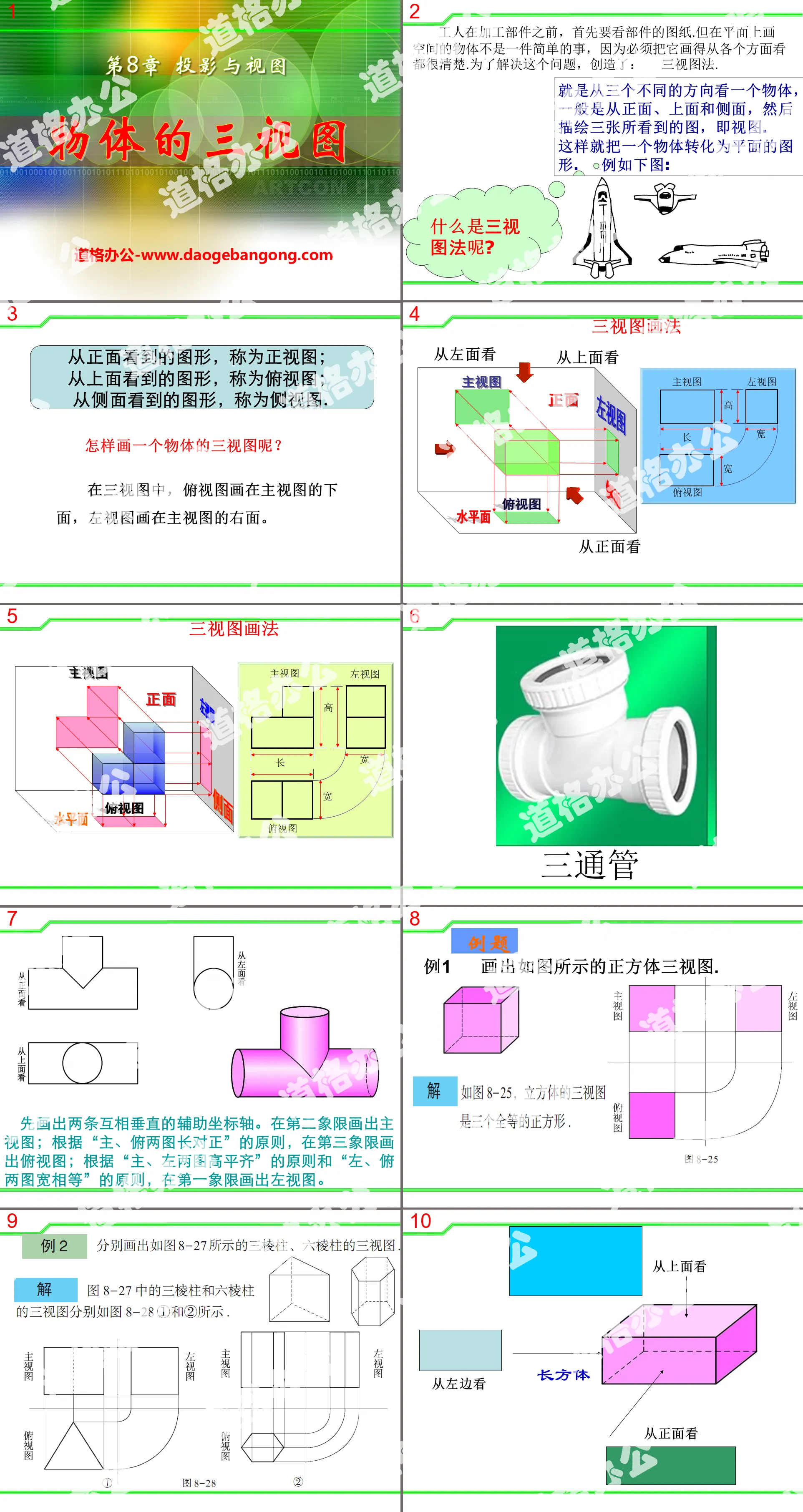
"Trois vues d'objets" Didacticiel PPT 2

Avant de traiter les pièces, ils doivent d'abord examiner les dessins des pièces. Mais dessiner un objet spatial sur un plan n'est pas une tâche simple, car il doit être dessiné clairement de tous les côtés. Afin de résoudre ce problème, nous l'avons créé. : Méthode à trois vues.

Qu'est-ce que la méthode à trois vues ?

Il s'agit de regarder un objet depuis trois directions différentes, généralement de face, de dessus et de côté, puis de dessiner trois images de ce que vous voyez, c'est-à-dire des vues.

Cela convertit un objet en un graphique plat. Par exemple, comme indiqué ci-dessous :

La figure vue de face est appelée vue de face ;

La figure vue de dessus est appelée vue de dessus ;

Une figure vue de côté est appelée vue de côté.

Comment dessiner trois vues d’un objet ?

Dans trois vues, la vue de dessus est dessinée sous la vue principale et la vue de gauche est dessinée à droite de la vue principale.

Dessinez d’abord deux axes de coordonnées auxiliaires mutuellement perpendiculaires. Dessinez la vue principale dans le deuxième quadrant ; dessinez une vue de dessus dans le troisième quadrant selon le principe de « l'alignement des hauteurs des images principale et inférieure » et dessinez la vue de dessus dans le troisième quadrant selon le principe de « l'image principale » ; les hauteurs des images principales et de gauche sont alignées" et le principe de "les hauteurs des images principales et inférieures sont alignées". Selon le principe de "largeur égale", dessinez la vue de gauche dans le premier quadrant.

Explorer

Utilisez des dés pour former la figure suivante. Observez cette figure de face, de gauche et du haut. Quelle figure plane pouvez-vous obtenir ?

résumé

1. Dessinez trois vues de la combinaison géométrique.

2. Dessinez les deux autres vues en fonction de la vue de dessus et du nombre de petits cubes.

3. Étant donné trois vues, trouvez le nombre total de petits cubes.

4. Après deux tentatives, trouvez le nombre maximum et minimum de petits cubes.

Opération

Cahier d'exercices : exercice 8.5

Questions 2, 3, 4 et 5 du groupe A.

Question 1 du groupe B.

Mots-clés : didacticiel d'enseignement à trois vues d'un objet, téléchargement du didacticiel PPT du volume de mathématiques de neuvième année de l'édition Qingdao, téléchargement du didacticiel de diapositives de mathématiques de neuvième année, téléchargement du didacticiel PPT à trois vues d'un objet, format .PPT ;

Pour plus d'informations sur le didacticiel PPT « Trois vues d'un objet », veuillez cliquer sur la balise ppt « Trois vues d'un objet ».

Didacticiel PPT « Trois vues d'objets » 3 :

"Trois vues d'objets" Didacticiel PPT 3 À faire 1. Les deux images présentées dans la figure sont des vues de dessus de la géométrie construite par plusieurs petits cubes. Les nombres dans les petits carrés représentent le nombre de petits cubes à cette position, s'il vous plaît. dessinez la vue de face et la vue de gauche de la géométrie correspondante. 2..

Didacticiel PPT « Trois vues d'objets » :

Didacticiel PPT « Trois vues d'objets » Devinez, pouvez-vous dire de quel type d'objet il s'agit en regardant simplement son ombre sous le soleil ? Dans la vie, nous devrions regarder et analyser une chose sous différents angles et aspects ? Trois vues : observation de graphiques d'objets, graphiques de projection orthographique.

文件信息

更新时间: 2024-10-28

本模板属于 数学课件 青岛版九年级数学下册 行业PPT模板

预览效果