"Intersecting Lines" PPT courseware Simple campus recruitment activity planning plan summary enterprise and institution recruitment publicity lecture PPT template is a general PPT template for business post competition provided by the manuscript PPT, simple campus recruitment activity planning plan summary enterprise and institution recruitment promotion Lecture PPT template, you can edit and modify the text and pictures in the source file by downloading the source file. If you want more exquisite business PPT templates, you can come to grid resource. Doug resource PPT, massive PPT template slide material download, we only make high-quality PPT templates!
| 文件名 如何下载使用 | 下载次数 | Download Points | 下载地址 |
|---|---|---|---|
| "Intersecting Lines" PPT... | 10275次 | 0.00 | Free Download |
Tips: If you open the template and feel that it is not suitable for all your needs, you can search for related content "Intersecting Lines" PPT courseware is enough.
How to use the Windows system template
Directly decompress the file and use it with office or wps
How to use the Mac system template
Directly decompress the file and use it Office or wps can be used
Related reading
For more detailed PPT-related tutorials and font tutorials, you can view: Click to see
How to create a high-quality technological sense PPT? 4 ways to share the bottom of the box
Notice
Do not download in WeChat, Zhihu, QQ, built-in browsers, please use mobile browsers to download! If you are a mobile phone user, please download it on your computer!
1. The manuscript PPT is only for study and reference, please delete it 24 hours after downloading.
2. If the resource involves your legitimate rights and interests, delete it immediately.
3. Contact information: service@daogebangong.com
"Intersecting Lines" PPT courseware, due to usage restrictions, it is only for personal study and reference use. For commercial use, please go to the relevant official website for authorization.
(Personal non-commercial use refers to the use of this font to complete the display of personal works, including but not limited to the design of personal papers, resumes, etc.)
Related reading
For more detailed PPT-related tutorials and font tutorials, you can view:Please click to see








Authoritative PPT Summary
"Intersecting Lines" PPT courseware
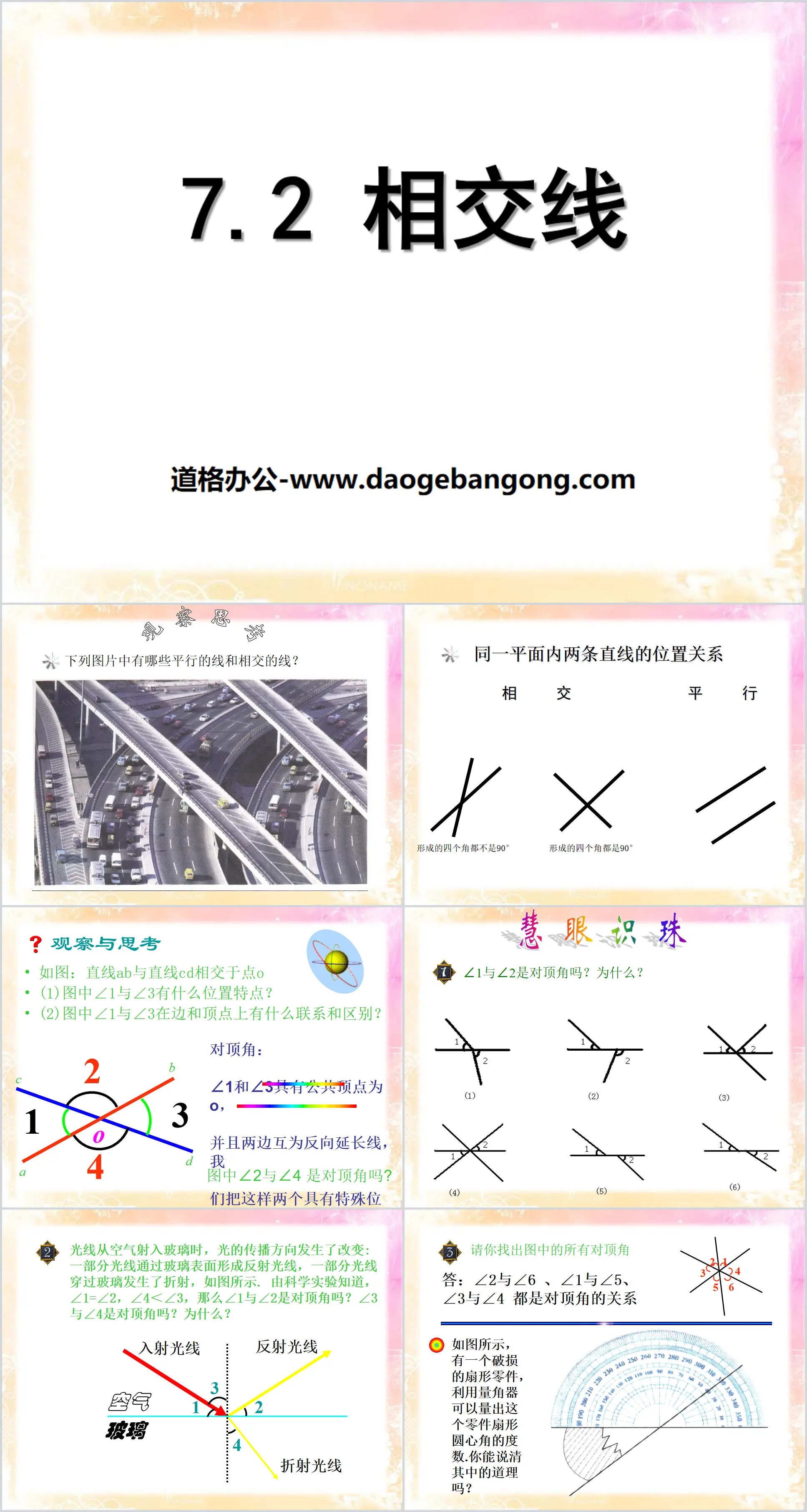
Part One: Observation and Thinking
As shown in the figure: Line AB and line CD intersect at point O
(1) What are the positional characteristics of ∠1 and ∠3 in the picture?
(2) What are the connections and differences between ∠1 and ∠3 on the edges and vertices in the figure?
Opposite top angle:
∠1 and ∠3 have a common vertex O, and the two sides are opposite extensions of each other. We call these two angles with special positions opposite vertex angles.
Intersecting lines PPT, the second part of the content: the eye of wisdom and knowledge
1.Are ∠1 and ∠2 opposite vertex angles? Why?
2. When light enters glass from the air, the propagation direction of the light changes: part of the light passes through the glass surface to form reflected light, and part of the light passes through the glass and is refracted, as shown in the figure. It is known from scientific experiments that ∠1=∠ 2, ∠4<∠3, then are ∠1 and ∠2 opposite vertex angles? Are ∠3 and ∠4 opposite vertex angles? Why?
3. Please find all the opposite vertex angles in the picture
Answer: ∠2 and ∠6, ∠1 and ∠5, ∠3 and ∠4 are all related to the vertex angles
Intersection line PPT, the third part: experimental research
(1) Purpose of the activity: Explore the properties of opposite vertex angles.
(2) Activity steps:
1. Observe: when a straight line rotates around point O, the changes of ∠1 and ∠2.
2. Conjecture: The relationship between ∠1 and ∠2.
3. Discussion: Please use appropriate methods to verify your conjecture. How many methods do you have?
Are the opposite vertex angles equal?
It is known that the two straight lines intersect at point O.
Prove: ∠1=∠3 ∠2=∠4
prove:
Because ∠1 and ∠2 are complementary, and ∠2 and ∠3 are complementary
So ∠1=∠3 (supplementary angles of the same angle are equal)
Similarly ∠2=∠4
Conclusion: Properties of opposite vertex angles: opposite vertex angles are equal
Intersecting lines PPT, part 4: do, do, practice
Please draw the corners that meet the following conditions based on the picture below:
⑴, and ∠ABC are opposite vertex angles;
⑵. It is the same angle as ∠ABC;
⑶, and ∠ABC are interior offset angles;
⑷, and ∠ABC are interior angles on the same side.
Fierce eyes and golden eyes
As shown on the right:
⑴. Point out the isotopic angle of ∠1;
⑵. Point out the interior angle of ∠2.
Isotropic angles: ∠1 and ∠CON, ∠1 and ∠EON
Internal offset angle: ∠2 and ∠NOF, ∠2 and ∠NOD
Keywords: Free download of Hebei Education Edition mathematics PPT courseware for seventh grade volume 2, intersecting lines PPT download, .PPT format;
For more information about the "Intersecting Lines" PPT courseware, please click on the "Intersecting Lines" ppt tab.
"Intersecting Lines" PPT:
"Intersecting Lines" PPT Part One: Situation Introduction In order to measure the intersection angle of the side walls of the paper cup, the clever Xiaohong designed the following plan. Can you explain the principle? Learning objectives 1. Understand the concept of antipodal angles and master the properties of antipodal angles. 2. Will identify the same...
"Supplementary Angle and Supplementary Angle" Parallel Lines and Intersecting Lines PPT Courseware 4:
"Complementary and Supplementary Angles" Parallel Lines and Intersecting Lines PPT Courseware 4 Complementary Angles Generally speaking, if the sum of two angles is equal to 90 (right angle), the two angles are said to be complementary angles to each other. That is, each angle is the supplementary angle of another angle. Please judge: (1)1+2=90, then 1 is the supplementary angle...
"Supplementary Angle and Supplementary Angle" Parallel Lines and Intersecting Lines PPT Courseware 3:
"Supplementary Angle and Supplementary Angle" Parallel Lines and Intersecting Lines PPT Courseware 3 Entering Life 1. What are the three interior angles of the triangle you usually use? What is the sum of two of the acute angles? 2. The picture shows a broken right-angled triangle. Can you find the broken corner?