
基本概念之数字信号处理DSP:采样后的时间信号频谱是周期性的,周期即为采样速度。
这个定理可以让我们形象地想象出如下图景:
- 在时域中进行的动态采样,等效于在频域中进行周期性延拓,这个周期等于时域的采样率。
关于这个结论,教科书中有很多推导方法,但我们今天从另一个角度来探讨这个问题:
通过离散傅里叶变换DFT解释这一原理
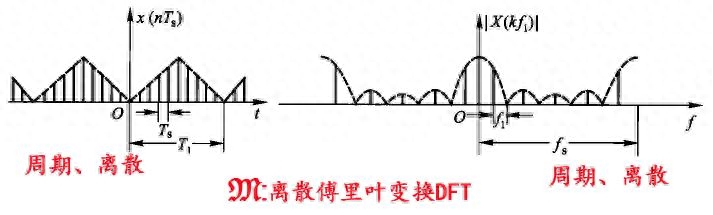
图1 离散傅里叶级数,截取一个周期变成DFT
现在我们给出定义:有限长序列的离散傅里叶变换。设有限长序列x(n)长度为N(在0≤n≤N-1范围内),它的离散傅里叶变换X(k)也是长度为N(在0≤k≤N-1范围内)的频域有限长序列。
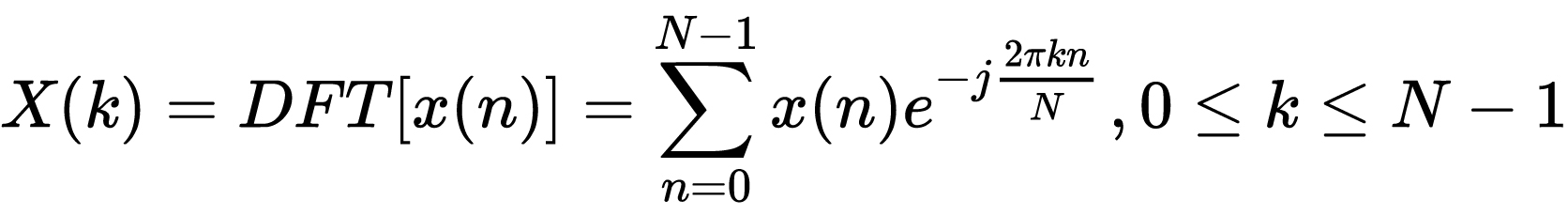
准确来说,离散X(k)是时间序列x(n)的离散频率谱。
- n为时间序号
- k为频率序号
- N为时间序列x(n)的样本点总数
图1中,我们只选择一个周期(主值序列)来观察,即为离散傅里叶变换DFT。
我们可以发现,时间与频率的关系如下:
- t=nTs②
- f=kf1=k/T1=k/NTs=kfs/N ③
其中,Ts是采样时间间隔(以秒为单位),fs=1/Ts为采样频率(以Hz为单位)。而且T1/Ts=N;
当n的范围为0到N-1时,k的取值范围取决于我们要计算X(k)的频率范围。例如,如果我们让k=0到N-1,等式③将产生f=0到fs(N-1)/N的频率范围,这是DFT的常规范围。
接下来,我们将在k=-2N到2N-1的更宽范围内评估X(k),这将产生f=-2fs到fs(2n-1)/N的频率范围。
假设一个长度为32的实值时间序列
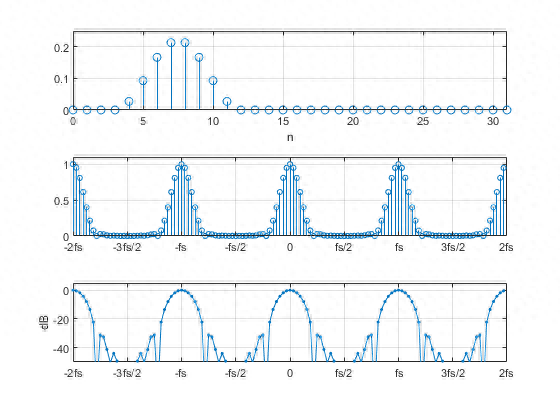
图1 DFT幅值图
图2展示了时间序列x(n)、对应的DFT幅值和dB-幅值。
如图2所示,频谱是周期性的,周期为fs。
关于频谱的周期性,我们可以直接从DFT方程中找到答案。
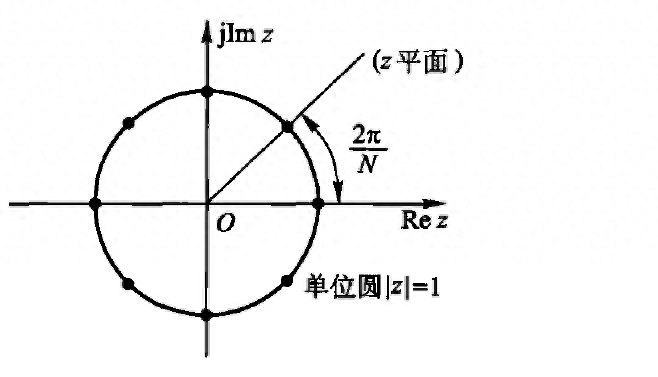
方程中存在一个复指数函数e,我们可以理解为:
将一个圆(2π)等分成N份,即2π/N,然后取第k个值,即2πk/N。
然后开始计算。
每算一圈(2π),循环再开始。
因此计算结果必然是周期性的,且周期为N。
如图3所示。最顶上的图显示了我们计算得到的DFT变换X(k)。
图3中间显示了k=0到N-1范围内的X(k);
图3底部的图只显示k=-N/2到N/2-1的样本,这是同样有效的范围。
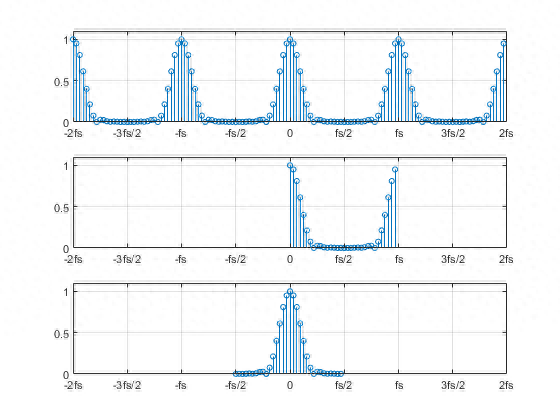
图3 放大看DFT
让我们看看在k=-N/2到N/2-1范围内计算的DFT。
图4展示了DFT的实数部分、虚数部分和幅度值。
图4说明了DFT的另一个属性:
对于实数序列x(n),DFT的实数部分为偶函数,虚数部分为奇函数。
这一属性在k=0到N-1范围内计算的DFT中同样适用,但在这种情况下,偶数和奇数是基于fs/2 Hz定义的,而不是0 Hz。
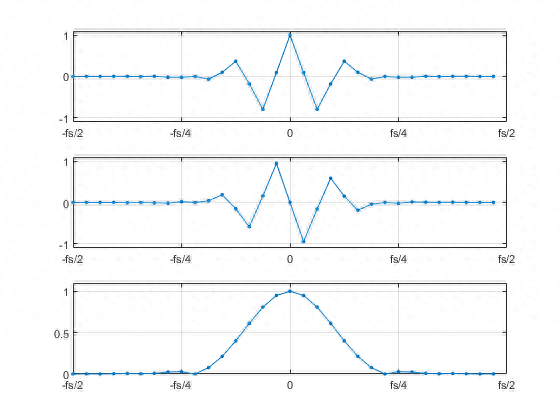
图4 从上到下依次为实数部分、虚数部分和幅值
如果您对此感兴趣,欢迎点赞和评论。
若需代码示例,请私信联系。
文章为用户上传,仅供非商业浏览。发布者:Lomu,转转请注明出处: https://www.daogebangong.com/articles/detail/shi-yu-shang-de-cai-yang-VS-pin-yu-shang-de-zhou-qi-yan-tuo-yong-li-san-fu-li-ye-bian-huan-zhi-guan-di-yan-shi.html

 支付宝扫一扫
支付宝扫一扫 
评论列表(196条)
测试